Interpolációs és regressziós feladatok scipy segítségével#
Interpoláció: A bemeneti adat pontpárjaihoz keressük egy adott függvény paramétereit, amely áthalad a megadott pontpárokon. A függvénynek megfelelő számú paraméterének kell lennie ahhoz, hogy képes legyen a pontpárokhoz tökéletesen illszkedni. Interpoláció során az adatpontok nem tekintjük hibával terheltnek. Tipikus gyakorlati alkalmazása az interpolációnak az ismeretlen adatpontok meghatározása: adat sűrítés, újra mintavételezés.
Regresszió: A bemeneti adat pontpárjaihoz keressük egy adott függvény paramétereit, mely a legjobban illeszkedik a pontpárokra. Ekkor a függvény egyenletét ismertnek tekintjük, és annak paramétereit határozzuk meg, oly módon, hogy a függvény és adatpontok közötti eltérést valamilyen szempontból minimalizáljuk. Amennyiben ezen eltérések a függő változóban normális eloszlást követnek, akkor az eltérések négyzeteinek összegét minimalizálva statistikailag optimális és torzítatlan becslést kapunk a függvény paramétereire. Ezt hívjuk legkisebb négyzetek módszerének. A regressziós modellekkel a gyakorlatban sok helyen találkozhatunk kezdve például a mérőállomással bemért fal pontokhoz illesztett sík mérnökgeodézia esetétől a mélytanulásos neurális hálókig, melyeket légi- vagy űrfelvétélek képi interpretációjához használhatnak a geoinformatikai gyakorlatban.
Interpoláció illetve regressziót végrehajthatunk egyváltozós, illetve többváltozós függvényeken is. Ismételjük át az analízis tárgyban tanult mérnöki szempontból releváns valós függvény típusokat:
Skalár-skalár függvények vagy egyváltozós valós függvények: Ezek a függvények az általonos iskolában tanult függvények, melyeknek bemenete egy szám, kimenete egy szám, vagy precízen fogalmazva a függvény értelmezési tartománya a valós számtest, és érték készlete is a valós számtest. A függvények álatlános tulajdonsága, hogy egy bemeneti értékhez csak egy kimeneti érték tartozhat, de egy kimeneti értékhez több bemeneti érték is, vagy precízen, egy értelmezési tartománybeli elemet a függvény pontosan egy darab értékészlet beli elemre képez le. Ezt a matematikábn szürjektív leképezének hívják. Így például a kör nem adható meg skalár-skalár függvény formában, hiszen, például az origó középpoontú egység sugarú kör az
X=0pontban azY=1ésY=-1pontokat venné fel, mely sérti a szürjektivítást.Vektor-skalár függvények vagy görbék: Ezek a függvények adnak meg tetszőleges görbét a síkon, vagy magasabb dimenziós térben. Bemenete egy szám, kimenete egy adott dimenziós vektor, vagy precízen fogalmazva a függvény értelmezési tartománya a valós számtest, és érték készlete a adott dimenziójú valós vektor tér. A bemeneti változót hívjuk a görbe paraméterének. Példaként említhetjük a kört, spirált, vagy akár az egyenes is megadható ebben a formában.
Skalár-vektor függvények vagy felületek: Ezek a függvényekkel adhatunk meg felületeket, például sík, ellipszoid, geoid, domborzat. A bemenete egy vektor a kimenete pedig egy szám, vagy precízen fogalmazva a függvény értelmezési tartománya egy adott dimenziójú valós vektor tér, és érték készlete a valós számtest.
Vektor-vektor függvények vagy vektor mezők: Ezen függvények bemenete egy adott dimenziójú vektor, és kimenete ugyancsak egy vektor, melynek dimenziója eltérhet a bemeneti vektor dimenziójától. Precízen fogalmazva a függvény értelmezési tartománya és érték készlete a valós vektor téren van definiálva. A bemeneti változót hívjuk a görbe paraméterének. Vektormezőre példa a gravitációs erőtér, mely megadja a Föld egy adott pontján (bemeneti vektor) a gravitáció irányát és nagyságát (kimeneti vektor).
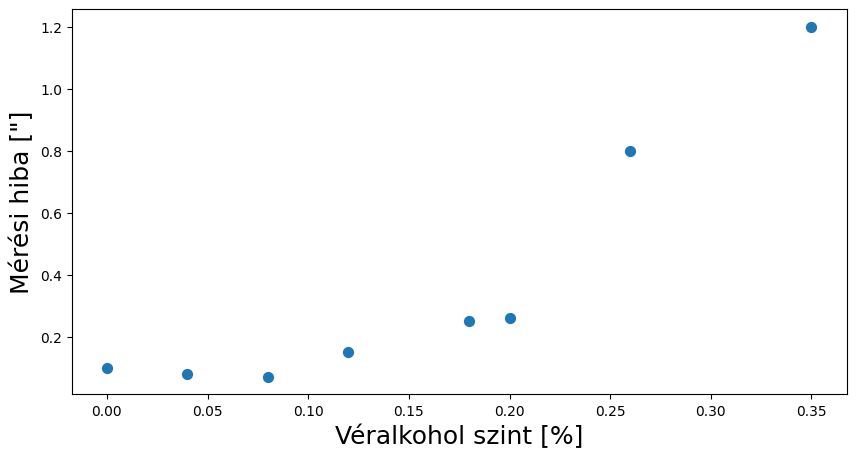
Példa: Alkohol hatása a mérés pontosságára#
import numpy as np
from matplotlib import pyplot as plt
data = np.loadtxt('data/bac.txt', delimiter=',', skiprows=1)
bac = data[:, 0]
measurement_error = data[:, 1]
plt.figure(figsize=(10, 5))
plt.scatter(bac, measurement_error, s=50)
plt.xlabel('Véralkohol szint [%]', fontsize=18)
plt.ylabel('Mérési hiba ["]', fontsize=18)
Text(0, 0.5, 'Mérési hiba ["]')
from scipy import interpolate
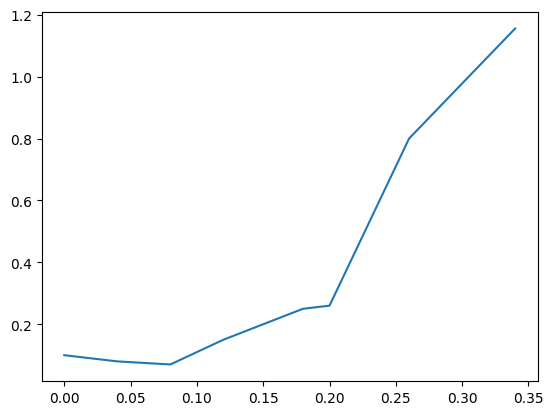
interp_lin = interpolate.interp1d(bac, measurement_error, kind='linear')
plt_x = np.arange(np.min(bac), np.max(bac), 0.01)
plt_y_lin = interp_lin(plt_x)
plt.plot(plt_x, plt_y_lin)
[<matplotlib.lines.Line2D at 0x7f997745e430>]
Interpolációs függvény típusok: https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.interp1d.html.
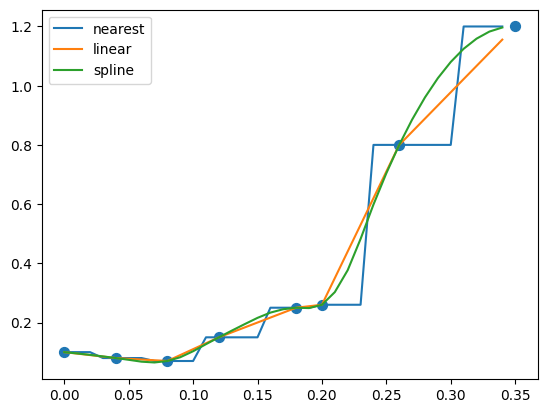
interp_nearest = interpolate.interp1d(bac, measurement_error, kind='nearest')
plt_y_nearest = interp_nearest(plt_x)
interp_spline = interpolate.interp1d(bac, measurement_error, kind='quadratic')
plt_y_spline = interp_spline(plt_x)
plt.scatter(bac, measurement_error, s=50)
plt.plot(plt_x, plt_y_nearest, label='nearest')
plt.plot(plt_x, plt_y_lin, label='linear')
plt.plot(plt_x, plt_y_spline, label='spline')
plt.legend()
<matplotlib.legend.Legend at 0x7f998ca56dc0>
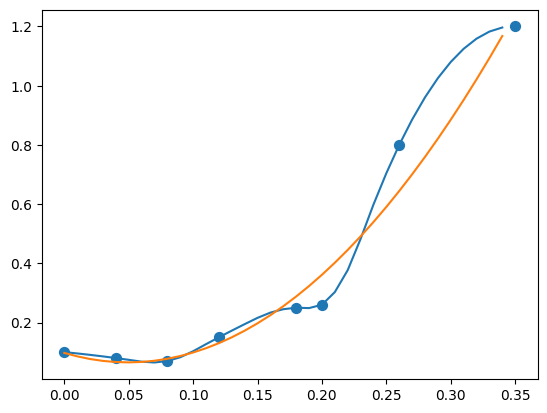
p = np.polyfit(bac, measurement_error, 2)
print(p)
[13.06445091 -1.29361931 0.09738621]
plt_y_reg = np.polyval(p, plt_x)
plt.scatter(bac, measurement_error, s=50)
plt.plot(plt_x, plt_y_spline, label='interpolation')
plt.plot(plt_x, plt_y_reg, label='regression')
[<matplotlib.lines.Line2D at 0x7f99753868e0>]
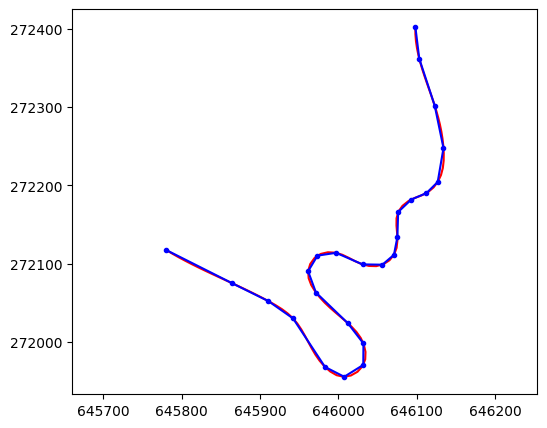
Példa: Trajektória interpolálása#
import numpy as np
data = np.loadtxt('data/path.txt')
x = data[:, 0]
y = data[:, 1]
dx = np.diff(x)
dy = np.diff(y)
dxy = np.vstack((dx, dy)).T
ds = np.linalg.norm(dxy, axis=1)
print(ds)
[94.43402988 51.81038988 38.53262773 74.05378923 27.58092457 28.67509721
27.34073152 32.7243961 56.45952975 28.91677714 23.26549806 24.019796
36.81807301 25.34315687 19.39478796 22.97334542 32.14555801 23.14344832
21.0079723 20.18132305 43.93595566 55.22353484 63.22393613 41.01468274]
s = np.cumsum(ds)
s = np.hstack((0, s))
print(s)
[ 0. 94.43402988 146.24441977 184.7770475 258.83083674
286.4117613 315.08685851 342.42759003 375.15198613 431.61151588
460.52829302 483.79379108 507.81358708 544.63166009 569.97481696
589.36960492 612.34295034 644.48850836 667.63195667 688.63992897
708.82125202 752.75720768 807.98074252 871.20467865 912.21936139]
import scipy.interpolate
int_x = scipy.interpolate.interp1d(s, x, kind="cubic")
int_y = scipy.interpolate.interp1d(s, y, kind="cubic")
plt.figure(figsize=(6,5))
s_d = np.linspace(s.min(), s.max(), 100)
x_d = int_x(s_d)
y_d = int_y(s_d)
plt.plot(x_d, y_d, 'r-')
plt.plot(x, y, 'b.-')
plt.axis('equal')
(645762.0274922663, 646152.1426624088, 271933.44999999995, 272424.93000000005)
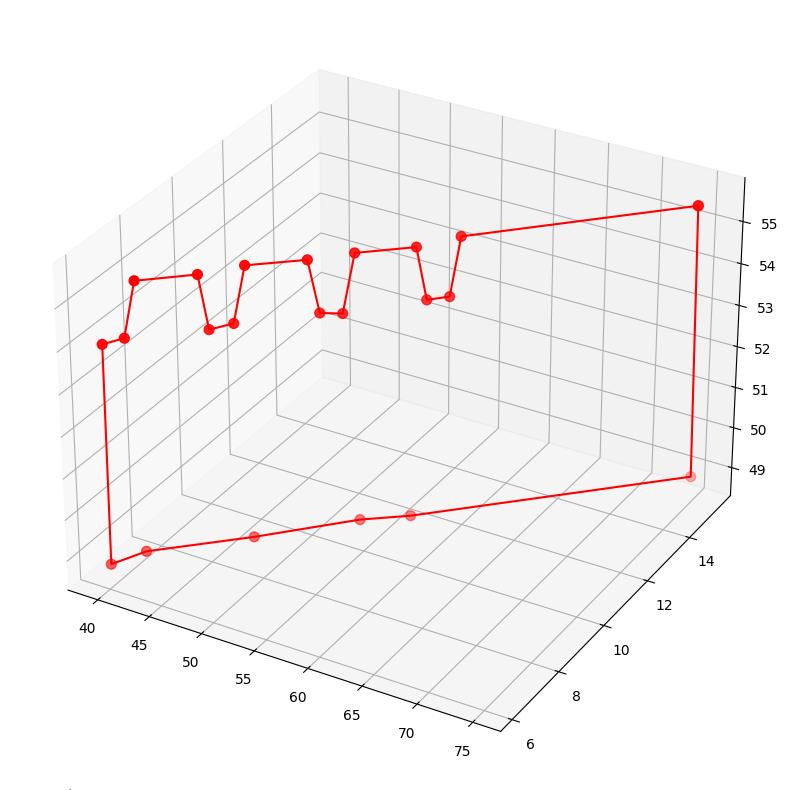
Példa: Sík vertikálistól való megfelelése#
import numpy as np
from matplotlib import pyplot as plt
from scipy.spatial.transform import Rotation

data = np.loadtxt('data/wall.csv', delimiter=',')
print(data[:5])
[[1.00000000e+00 5.80117481e+06 3.09715239e+05 5.55370000e+01]
[3.00000000e+00 5.80116053e+06 3.09711634e+05 5.54790000e+01]
[4.00000000e+00 5.80115994e+06 3.09711431e+05 5.41250000e+01]
[5.00000000e+00 5.80115862e+06 3.09711062e+05 5.41300000e+01]
[6.00000000e+00 5.80115794e+06 3.09710929e+05 5.53750000e+01]]
points = data[:, 1:4]
print(points[:5])
[[5.80117481e+06 3.09715239e+05 5.55370000e+01]
[5.80116053e+06 3.09711634e+05 5.54790000e+01]
[5.80115994e+06 3.09711431e+05 5.41250000e+01]
[5.80115862e+06 3.09711062e+05 5.41300000e+01]
[5.80115794e+06 3.09710929e+05 5.53750000e+01]]
plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
ax.plot3D(points[:,0], points[:,1], points[:,2], 'r-')
ax.scatter3D(points[:,0], points[:,1], points[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f9975214910>
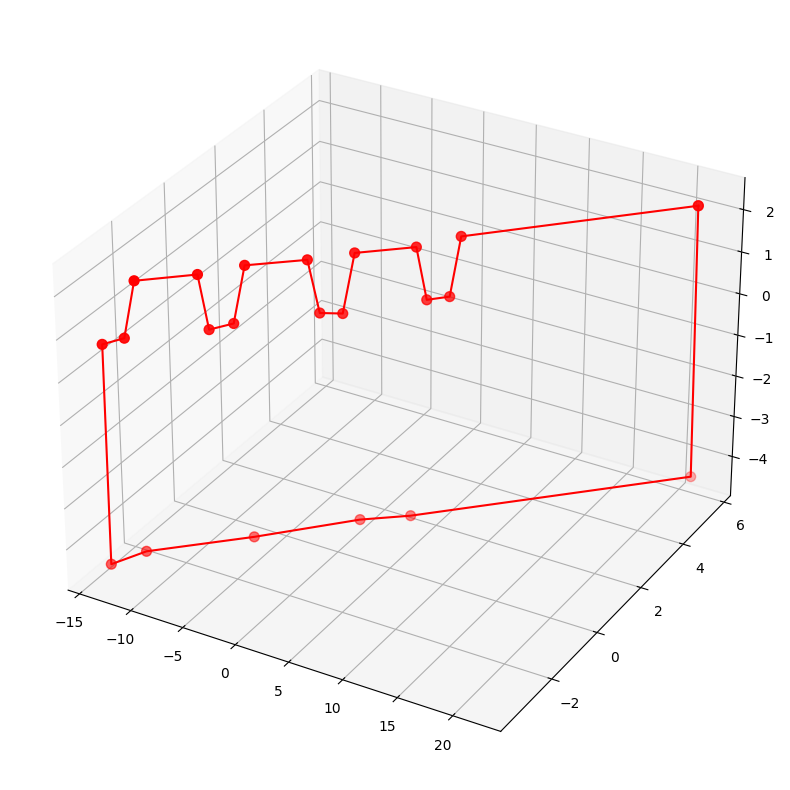
Előzetes transzformációk#
centroid = np.mean(points, axis=0)
points_c = points - centroid
plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
ax.plot3D(points_c[:,0], points_c[:,1], points_c[:,2], 'r-')
ax.scatter3D(points_c[:,0], points_c[:,1], points_c[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f9974aaec40>
R_local = Rotation.from_euler('xyz', [90, 0, 0], degrees=True).as_matrix()
points_c_r = points_c @ R_local
plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
ax.plot3D(points_c_r[:,0], points_c_r[:,1], points_c_r[:,2], 'r-')
ax.scatter3D(points_c_r[:,0], points_c_r[:,1], points_c_r[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f99752daa90>
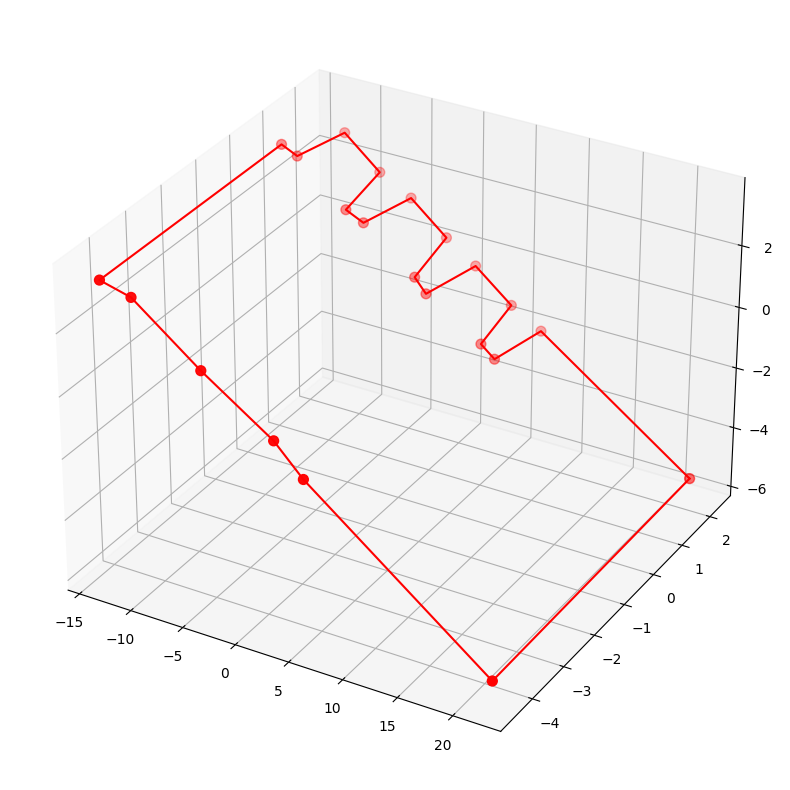
Sík illesztés legkisebb négyzetek módszerével#
p_x = points_c_r[:, 0]
p_y = points_c_r[:, 1]
p_z = points_c_r[:, 2]
A = np.vstack((p_x, p_y, np.ones(p_x.shape[0]))).T
b = p_z
x = np.linalg.inv(A.T @ A) @ A.T @ b
print(x)
[-2.57808734e-01 -8.06262847e-03 -1.53425717e-10]
v = A @ x - b
print(v)
[-0.04046585 0.03702611 -0.00243432 -0.0311671 0.00110487 -0.00407598
0.01300006 0.00753676 0.0052719 -0.00116173 -0.00911155 0.00965221
0.04257735 0.01515368 -0.00052857 -0.00070917 0.01490353 -0.02950146
-0.027716 -0.04853021 -0.00248655 0.09212787 -0.04046585]
plane = lambda X, Y: x[0]*X + x[1]*Y + x[2]
minx, maxx = points_c_r[:, 0].min(), points_c_r[:, 0].max()
miny, maxy = points_c_r[:, 1].min(), points_c_r[:, 1].max()
minz, maxz = points_c_r[:, 2].min(), points_c_r[:, 2].max()
X_viz, Y_viz = np.meshgrid(np.arange(minx, maxx, 0.5), np.arange(miny, maxy, 0.5))
Z_viz = plane(X_viz, Y_viz)
fig = plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
ax.plot_surface(X_viz, Y_viz, Z_viz, rstride=1, cstride=1, alpha=0.2)
ax.scatter3D(points_c_r[:,0], points_c_r[:,1], points_c_r[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f99750a32e0>
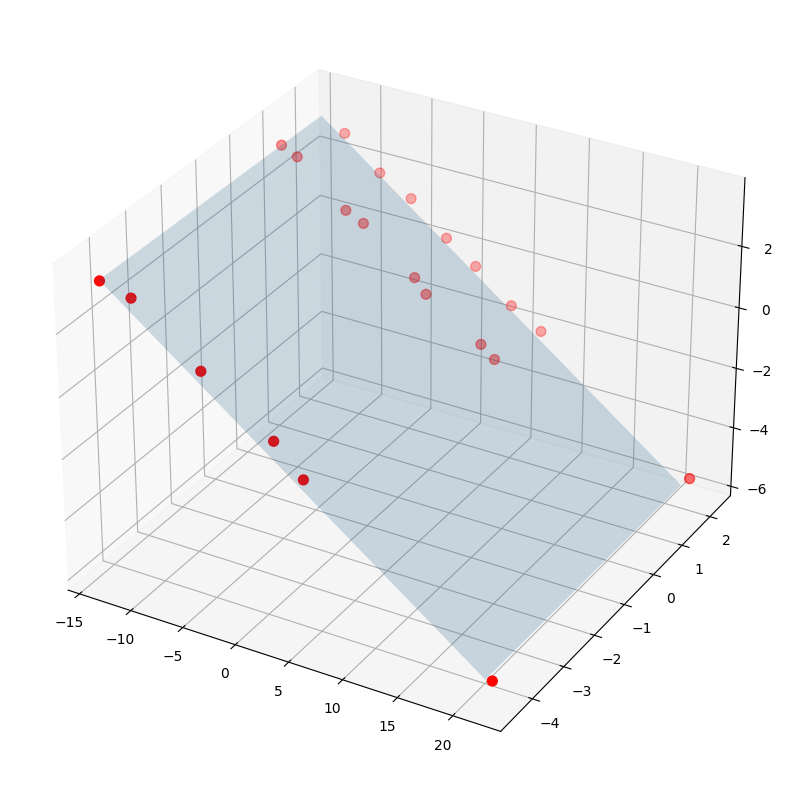
Sík illesztése SVD felbontással#
Megoldás SVD felbontással a következő:
Először a centroidi koordináták mátrixának összeszorozzuk önmaga transzponáltjával, ezzel előállítva egy “kovariancia” jellegű mátrixot.
Ezután elpállítjuk az SVD felbontást,
Majd az U mátrix jobb oldali vektor adja meg a legkisebb értelemben legjobban illeszkedő sík normálisát.
D = points_c_r.T @ points_c_r
[U, S , V] = np.linalg.svd(D)
n = U[:, -1]
A normálist kicsit átalakítjuk hogy a korábbi sík egyenletbe illeszkedjen:
# a(x-x0) + b(y-y0) + c(z-z0) = 0, where n = [a, b, c]
# if (x0, y0, z0) = (0,0,0), then z = (-ax-by)/c
plane_svd = lambda X, Y: (-n[0]*X -n[1]*Y) / n[2]
Ellenőrizhetjük, hogy ez tényleg egy normális:
z_plane_r = plane_svd(points_c_r[:, 0], points_c_r[:, 1])
check_normal = 0
for k in range(len(points_c_r)):
p_plane = np.array([points_c_r[k, 0], points_c_r[k, 1], z_plane_r[k]])
check_normal += np.abs(np.dot(p_plane, n))
print(check_normal)
1.6766530209094517e-15
minx, maxx = points_c_r[:, 0].min(), points_c_r[:, 0].max()
miny, maxy = points_c_r[:, 1].min(), points_c_r[:, 1].max()
minz, maxz = points_c_r[:, 2].min(), points_c_r[:, 2].max()
X_viz, Y_viz = np.meshgrid(np.arange(minx, maxx, 0.5), np.arange(miny, maxy, 0.5))
Z_viz = plane_svd(X_viz, Y_viz)
fig = plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
ax.plot_surface(X_viz, Y_viz, Z_viz, rstride=1, cstride=1, alpha=0.2)
ax.scatter3D(points_c_r[:,0], points_c_r[:,1], points_c_r[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f9974f8f550>
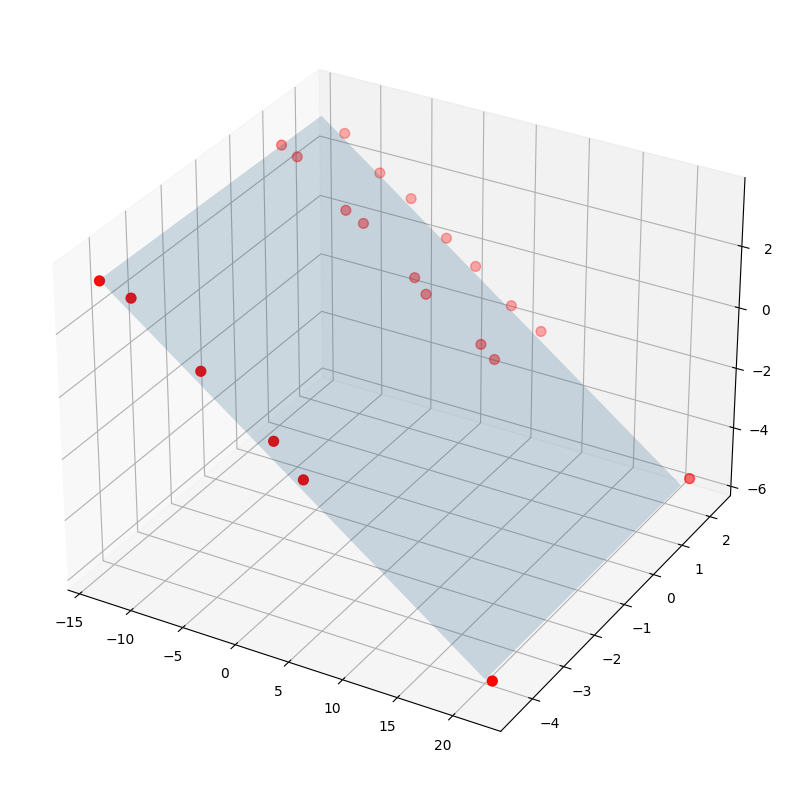
Hiba analízis#
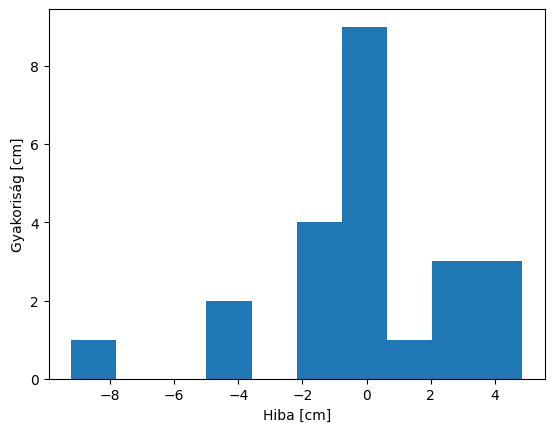
dz = points_c_r[:, 2] - plane(points_c_r[:, 0], points_c_r[:, 1])
plt.hist(dz*100, bins=10)
plt.xlabel('Hiba [cm]')
plt.ylabel('Gyakoriság [cm]')
Text(0, 0.5, 'Gyakoriság [cm]')
print('Legikisebb hiba: ', np.min(dz))
print('Legikisebb abszolút hiba: ', np.min(np.abs(dz)))
print('Legnagyobb hiba: ', np.max(dz))
print('Legnagyobb abszolút hiba: ', np.max(np.abs(dz)))
Legikisebb hiba: -0.092127874897308
Legikisebb abszolút hiba: 0.0005285705269182372
Legnagyobb hiba: 0.048530210663125906
Legnagyobb abszolút hiba: 0.092127874897308
print('Átlagos hiba: ', np.mean(dz))
print('Átlagos abszolút hiba (MAE): ', np.mean(np.abs(dz)))
print('Szórás: ', np.std(dz))
rmse = np.sqrt(np.sum(np.power(dz, 2)) / len(dz))
print('Középhiba (RMSE): ', rmse)
Átlagos hiba: 6.033820786006285e-19
Átlagos abszolút hiba (MAE): 0.02072646505129827
Szórás: 0.030090421173322376
Középhiba (RMSE): 0.030090421173322376
Kérdés: a szórás és az középhiba ugyanaz? Vizsgáljuk meg. Tegyük fel, hogy az illesztett sík egy méterrel feljebb helyezkedik el mint amit meghatároztunk. Ez egy extrém eset, de előfordulhat ha egy nagyon nagy kiugró érték szerepel az adatokban. Most ezt csak szimuláljuk azzal, hogy a dz vektorhoz egyet hozzáadunk:
dz_bias = dz + 1
plt.hist(dz_bias)
(array([1., 0., 0., 2., 0., 4., 9., 1., 3., 3.]),
array([0.90787213, 0.92193793, 0.93600374, 0.95006955, 0.96413536,
0.97820117, 0.99226698, 1.00633278, 1.02039859, 1.0344644 ,
1.04853021]),
<BarContainer object of 10 artists>)
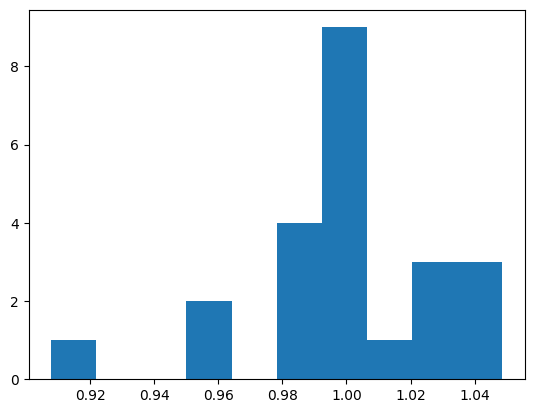
Nézzük meg így a hibákat jellemző mérőszámainkat:
print('Átlagos hiba: ', np.mean(dz_bias))
print('Szórás: ', np.std(dz_bias))
rmse = np.sqrt(np.sum(np.power(dz_bias, 2)) / len(dz))
print('Középhiba vagy RMSE: ', rmse)
Átlagos hiba: 1.0
Szórás: 0.030090421173322387
Középhiba vagy RMSE: 1.0004526142933448
Tehát a szórás az átlag körüli ingadozást méri, míg a középhiba a mért és becsült model közötti ingadozást írja le. A középhiba így felfogható az átlagos hiba és a szórás eredőjének. Amennyiben az átlagos hiba alacsony, akkor a szórás megegyezik az középhibával.
Most vizsgáljuk meg az átlagos eltéréseket és a mediánt:
print('Átlagos hiba: ', np.mean(dz))
print('Átlagos abszolút hiba (MAE): ', np.mean(np.abs(dz)))
print('Medián hiba: ', np.median(dz))
print('Medián abszolót hiba: ', np.median(np.abs(dz)))
Átlagos hiba: 6.033820786006285e-19
Átlagos abszolút hiba (MAE): 0.02072646505129827
Medián hiba: 0.0007091674770802747
Medián abszolót hiba: 0.013000062433472584
print('Átlagos hiba: ', np.mean(dz_bias))
print('Átlagos abszolút hiba (MAE): ', np.mean(np.abs(dz_bias)))
print('Medián hiba: ', np.median(dz_bias))
print('Medián abszolót hiba: ', np.median(np.abs(dz_bias)))
Átlagos hiba: 1.0
Átlagos abszolút hiba (MAE): 1.0
Medián hiba: 1.0007091674770803
Medián abszolót hiba: 1.0007091674770803
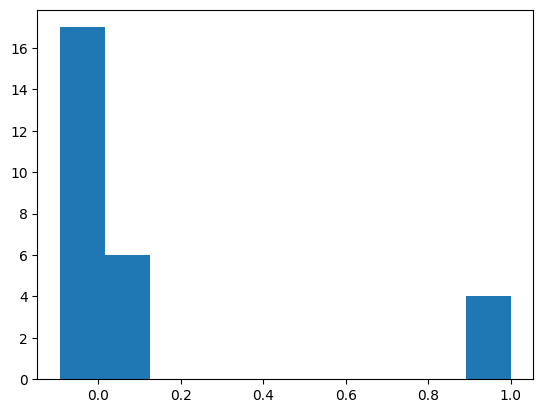
dz_gross = np.hstack((dz, np.array([1.0, 1.0, 1.0, 1.0])))
plt.hist(dz_gross)
(array([17., 6., 0., 0., 0., 0., 0., 0., 0., 4.]),
array([-0.09212787, 0.01708491, 0.1262977 , 0.23551049, 0.34472328,
0.45393606, 0.56314885, 0.67236164, 0.78157443, 0.89078721,
1. ]),
<BarContainer object of 10 artists>)
print('Átlagos hiba: ', np.mean(dz_gross))
print('Átlagos abszolút hiba (MAE): ', np.mean(np.abs(dz_gross)))
print('Medián hiba: ', np.median(dz_gross))
print('Medián abszolút hiba: ', np.median(np.abs(dz_gross)))
Átlagos hiba: 0.14814814814814814
Átlagos abszolút hiba (MAE): 0.16580402578443926
Medián hiba: 0.0024343160611965953
Medián abszolút hiba: 0.015153675546118794
A nem nulla átlagos és átlagos abszolút hiba modell bias hibát sejtet. Az átlagos és medián hiba nagy különbsége viszont egyértelműen durva hibás mérések jelenlétét jelzi. A bias hiba itt a kiugró mérési hibákból fakad.
print('Hiba 95-ös percentilisen: ', np.percentile(dz, 95))
Hiba 95-ös percentilisen: 0.0404658522947523
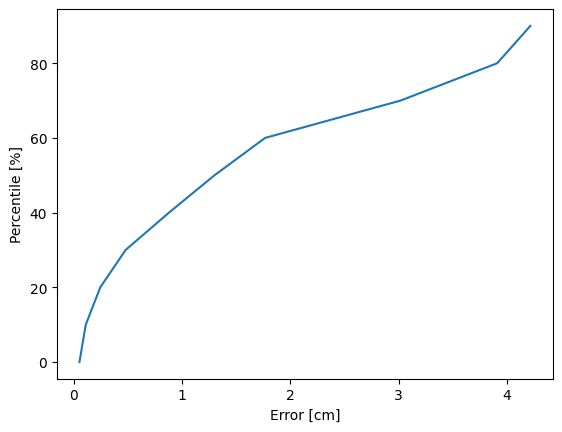
percentiles = []
for pcnt in np.arange(0, 100, 10):
percentiles.append([pcnt, np.percentile(np.abs(dz), pcnt)])
percentiles = np.array(percentiles)
plt.plot(percentiles[:, 1]*100, percentiles[:, 0])
plt.xlabel('Error [cm]')
plt.ylabel('Percentile [%]')
Text(0, 0.5, 'Percentile [%]')
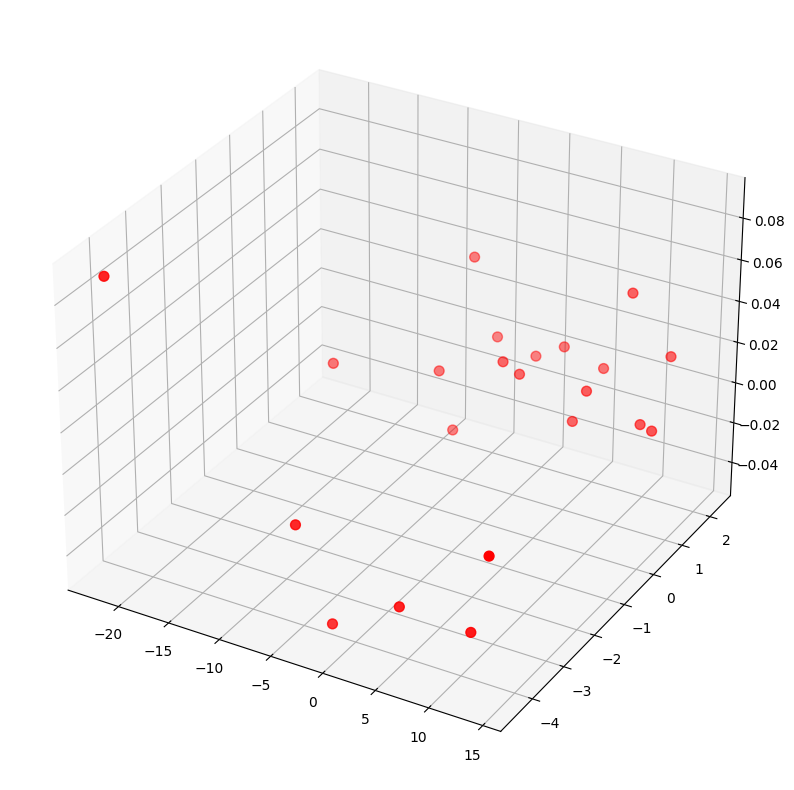
Becsült sík transzformálása XY síkra#
b0 = np.array([0, 0, plane(0, 0)])
b1 = np.array([-1, 0, plane(-1, 0)])
b2 = np.array([0, 1, plane(0, 1)])
v1 = b1 - b0
v1 = v1 / np.linalg.norm(v1)
print('v1 = ', v1)
v2 = b2 - b0
v2 = v2 / np.linalg.norm(v2)
print('v2 = ', v2)
v3 = np.cross(v1, v2)
v3 = v3 / np.linalg.norm(v3)
print('v3 = ', v3)
B = np.vstack((v1, v2, v3))
v1 = [-0.96833722 0. 0.24964579]
v2 = [ 0. 0.9999675 -0.00806237]
v3 = [-0.24963819 -0.00780711 -0.96830771]
points_c_r_p = points_c_r.copy()
points_c_r_p = points_c_r_p @ np.linalg.inv(B)
fig = plt.figure(figsize=(12,10))
ax = plt.axes(projection='3d')
#ax.plot_surface(X, Y, Z, rstride=1, cstride=1, alpha=0.2)
ax.scatter3D(points_c_r_p[:,0], points_c_r_p[:,1], points_c_r_p[:,2], c='r', s=50)
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f99740583d0>
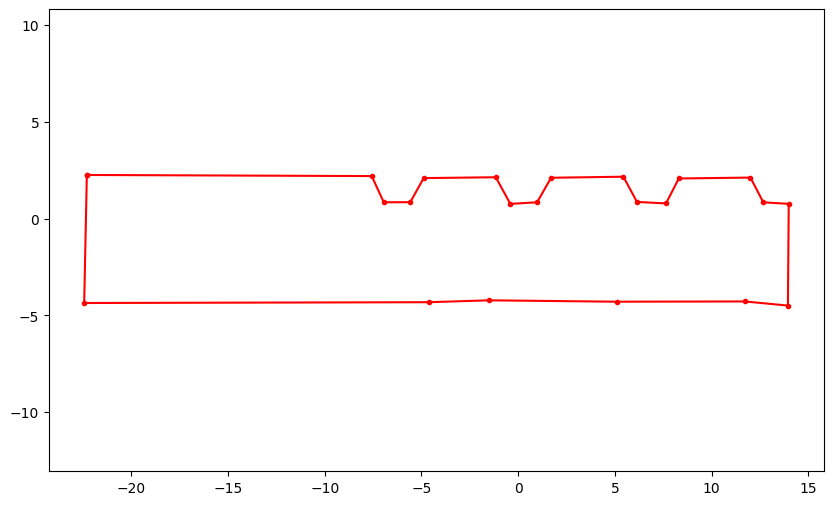
plt.figure(figsize=(10,6))
plt.plot(points_c_r_p[:, 0], points_c_r_p[:, 1], 'r.-')
plt.xlim([-5, 5])
plt.axis('equal')
(-24.25409826136906,
15.813126635108343,
-4.833716986214311,
2.5943640045672507)
points_hat_c_r_p = points_c_r.copy()
points_hat_c_r_p[:, 2] = z_plane_r
points_hat_c_r_p = points_hat_c_r_p @ np.linalg.inv(B)
print('chk z (~=0): ', np.sum(np.abs(points_hat_c_r_p[:, 2])))
chk z (~=0): 0.00036530823860780973