Transzformációk

Ebben a fejezetben megismerkedünk, hogyan tudunk geometriai alakzatokat forgatni síkon és térben.

Geometria reprezentálása

import numpy as np
import matplotlib.pyplot as plt

Első lépésként meg kell határoznunk, hogy tudjuk reprezentálni alakzatokat. Síkon először a pontok koordinátáit gyűjtük egy \(n \times 2\)-es tömbbe adjuk meg, tehát a pontok koordinátái sorokba vannak rendezve:

pt = np.array([[1, 1], [2, 1], [2, 2], [1, 2], [1, 1]])

Ezután a pontokat egyszerűen ki tudjuk rajzolni:

plt.figure(figsize=(3, 3))
plt.plot(pt[:, 0], pt[:, 1], 'r.-')
plt.grid()
plt.gca().set_aspect('equal')

Figyelem

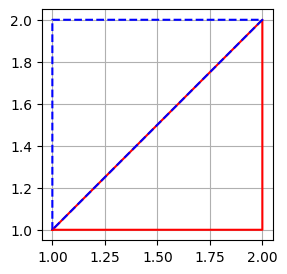
A pontok sorrendjére oda kell ügyelnünk, ugyanis a pontok a sorok sorrendjébe lesznek összekötve. Például próbáljuk ki, hogy nézz ki az alakzat, ha a második és harmadik pontot felcseréljük a fenti példában:

pt = np.array([[1, 1], [2, 2], [2, 1], [1, 2], [1, 1]])
plt.figure(figsize=(3, 3))
plt.scatter(pt[:, 0], pt[:, 1])
plt.plot(pt[:, 0], pt[:, 1])

Tipp

Ökölszabályként a pontokat órajárásval megegyező vagy ellentétes módon adjuk meg.

Figyelem

A pontok tömbjének az utolsó eleme a pont listának az első elemének kell lennie ahhoz, hogy az utolsó pont az első ponttal is össze legyen kötve, és így négyzetet kapjunk.

Ha a pontok összekötése a pontok sorrendjében történik, akkor a pontok sorrendjének megváltoztatásával azt meg tudjuk változtatni. Ehhez használhatunk egy index listát. Például a második és harmadik pont sorrendje az alábbi módon megváltoztatható:

pt = np.array([[1, 1], [2, 1], [2, 2], [1, 2], [1, 1]])
print('Eredeti lista:\n', pt)

idx = [0, 2, 1, 3, 4] # index lista
print('Megkevert lista:\n', pt[idx, :])

Eredeti lista:
 [[1 1]
 [2 1]
 [2 2]
 [1 2]
 [1 1]]
Megkevert lista:
 [[1 1]
 [2 2]
 [2 1]
 [1 2]
 [1 1]]

Az index lista használatával elkerülhető az első elem ismétlése az utolsó helyen:

pt = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

plt.figure(figsize=(3, 3))
plt.plot(pt[idx, 0], pt[idx, 1], 'r.-')
plt.grid()
plt.gca().set_aspect('equal')

Ezzel ugyanazt az ábrát kaptuk, mint korábban. Vegyük észre, hogy a pt egy pontokat tartalmazó tömb, és az idx index lista adja meg a négyszöget alakját. Ezzel szétválasztottuk, a geometriát (pontok) és az azok közötti kapcsolatot leíró topológiát. Hasonló módon léterhozhatóak komplexebb alakzatok. Például az előbbi pontokat használva megadhatunk két háromszöget:

pt = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
tri1 = [0, 1, 2, 0]
tri2 = [0, 3, 2, 0]

plt.figure(figsize=(3, 3))
plt.plot(pt[tri1, 0], pt[tri1, 1], 'r-')
plt.plot(pt[tri2, 0], pt[tri2, 1], 'b--')
plt.grid()
plt.gca().set_aspect('equal')

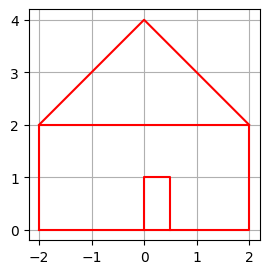
Az alábbi példában kirajzolunk egy házikót:

pt = np.array([[-2, 0],  # 0
                [2, 0],  # 1
                [2, 2],  # 2
                [-2, 2], # 3
                [0, 4],  # 4
                [0, 0],  # 5
                [0, 1],  # 6
                [0.5, 1],# 7
                [0.5, 0] # 8
              ]) 

walls = [0, 1, 2, 3, 0]
roof = [3, 4, 2]
door = [5, 6, 7, 8]

plt.figure(figsize=(3, 3))
plt.plot(pt[walls, 0], pt[walls, 1], 'r-')
plt.plot(pt[roof, 0], pt[roof, 1], 'r-')
plt.plot(pt[door, 0], pt[door, 1], 'r-')
plt.grid()
plt.gca().set_aspect('equal')

Transzformációk síkon

Eltolás

Egy \(p \in \mathbb{R}^2\) pontot az alábbi módon tudunk eltolni:

\(q = p + t\),

ahol \(t \in \mathbb{R}^2\) az eltolás vektora.

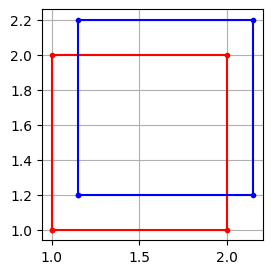
Toljuk el a korábbi négyszöget 0.15-tel az X és 0.2-vel az Y tengelyek irányában:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

t = [0.15, 0.2]
q = p + t

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

Skálázás

Egy \(p \in \mathbb{R}^2\) pontot az alábbi módon tudunk nagyítani, vagy kicsinyíteni:

\(q = st\),

ahol \(s \in \mathbb{R}\) egy szám mely a nagyítás vagy kicsinyítés méretét adja meg. Ha \(0 < s <1\) akkor kicsinyítést, ha \(1 < s\) akkor nagyítást végzünk.

Az alábbi példában a négyszöget 1.5-szeresére nagyítjuk és 0.5-szeresére kicsinyítjük:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

q_small = 1.5*p
q_big = 0.5*p

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q_small[idx, 0], q_small[idx, 1], 'g.-')
plt.plot(q_big[idx, 0], q_big[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

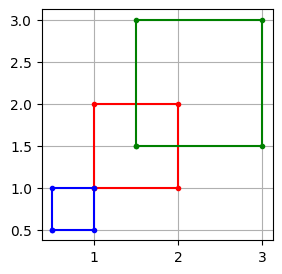
Vegyük észre, hogy a méretarány változtatás nem a négyszög középpontjában történt. Ha a nagyítást vagy kicsinyítést az alakzat középpontában szeretnénk elvégezni, akkor három lépést kell elvégezni:

• Az alakzatot az origóba kell tolnunk a súlypont koordinátáinak segítségével,

• Majd a skálázást végre kell hajtatnunk,

• Végül a kapott pontokat vissza kell tolnunk az eredeti súlypontba.

Végezzük el ezeket a lépéseket külön-külön és nézzük meg mik az éppen aktuális pontok koordinátái.

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0)
q = p - t

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

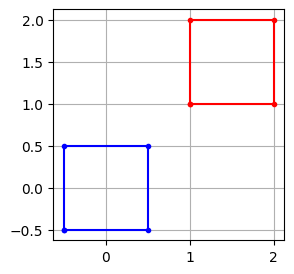
p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0)
q = 1.5 * (p - t)

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

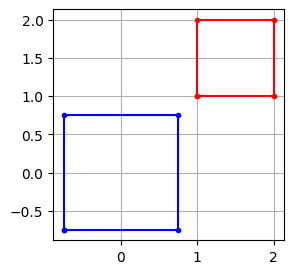
p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0) # Súlypont koordinátái
q = 1.5 * (p - t) + t

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

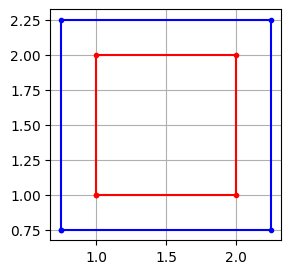
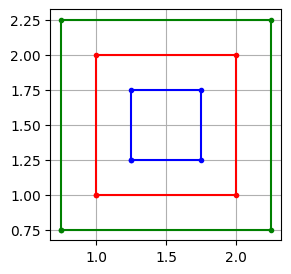
Végül kicsinyítés és nagyítás a sólypont körül:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0)

q_small = 1.5*(p - t) + t
q_big = 0.5*(p - t) + t

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q_small[idx, 0], q_small[idx, 1], 'g.-')
plt.plot(q_big[idx, 0], q_big[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

Forgatás

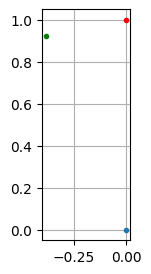
from math import sin, cos

alpha = np.deg2rad(22.5) # = / 180.0 * math.pi
R = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])
print(R)

[[ 0.92387953 -0.38268343]
 [ 0.38268343  0.92387953]]

p = np.array([0, 1])
q = R @ p
print(q)

[-0.38268343  0.92387953]

plt.figure(figsize=(3, 3))
plt.plot(0, 0, '.')
plt.plot(p[0], p[1], 'r.')
plt.plot(q[0], q[1], 'g.')
plt.grid()
plt.gca().set_aspect('equal')

A forgatási mátrix úgynevezett ortonormált mátrix. Ez azt jelenti, hogy a mátrix transzponáljta megegyezik az inverzével:

np.linalg.inv(R) - R.T

array([[0.00000000e+00, 5.55111512e-17],
       [0.00000000e+00, 0.00000000e+00]])

Használjatuk a mátrix normát, hogy ellenőrizzük, hogy két mátrix megegyezik:

np.linalg.norm(np.linalg.inv(R) - R.T)

5.551115123125783e-17

Azon kívül hogy, a forgatási mátrix transzponáltja megegyezik inverzével, az ortonormáltság azt is jelenti, hogy a forgatási mátrix determinánsa 1:

np.linalg.det(R)

1.0

Következmény, hogy a forgatási mátrix önmagával vett inverze az egységmátrix:

np.linalg.inv(R) @ R

array([[ 1.00000000e+00,  2.96506192e-17],
       [-2.16349973e-17,  1.00000000e+00]])

Nyilvánvalóan ez igaz a transzponáltra is:

R.T @ R

array([[ 1.00000000e+00, -2.16349973e-17],
       [-2.16349973e-17,  1.00000000e+00]])

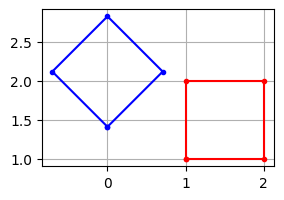
Ezek után alkalmazzuk a forgatást a a négyszögre (figyeljünk oda a pont mátrixok és a forgatási mátrix méreteire):

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

alpha = np.deg2rad(45)
R = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])

q = (R @ p.T).T

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

Vizsgáljuk meg a q = (R @ p.T).T műveletet és a vektorok és mátrixok alakját:

print(p.shape)
print(p.T.shape)
print((R @ p.T).shape)
print((R @ p.T).T.shape)

(4, 2)
(2, 4)
(2, 4)
(4, 2)

A műveletek végén a transzformált pontoknak sorokba kell rendezve lennie.

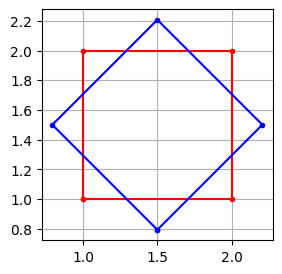
Vegyük észre a fenti példában a forgatás nem a négyszög súlypontja körül történt. A súlypont körüli forgatáshoz a skálázáshoz hasonlóan kell eljárnunk: a pontokat az origóba toljuk, ott a forgatást elvégezzük, majd vissze toljuk az alakzatot az eredeti súlypontba.

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

alpha = np.deg2rad(45)
R = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])

t = np.mean(p, axis=0)
q = (R @ (p - t).T).T + t

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

Összetett transzformációk homogén koordinátákkal

Nagyítsuk az alakzatot 1.5-szeresére a saját súlypontjából nézve, ls forgassuk el 22 fokkal, majd toljuk el az alakzatot -1.5 egységgel az Y tengely mentén:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
idx = [0, 1, 2, 3, 0]

alpha = np.deg2rad(22)
R = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])
t = np.mean(p, axis=0)
q = (1.5 * R @ (p - t).T).T + t + [0, -1.5]

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

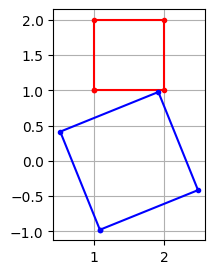
A pontok homogén koordinátáit úgy kapjuk, hogy eggyel megnöveljük a pontok dimenzióját, és a megnövelt dimenzió helyére 1-t írunk:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
p_ = np.hstack((p, np.ones((p.shape[0], 1))))

print(p_)

[[1. 1. 1.]
 [2. 1. 1.]
 [2. 2. 1.]
 [1. 2. 1.]]

Írjuk fel a fenti transzformációkat homogén koordinátákkal és transzformációkkal:

p = np.array([[1, 1], [2, 1], [2, 2], [1, 2]])
p_ = np.hstack((p, np.ones((p.shape[0], 1))))

idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0)
T_ = np.array([[1, 0, t[0]],
               [0, 1, t[1]],
               [0, 0, 1]])

T_inv_ = np.array([[1, 0, -t[0]],
                   [0, 1, -t[1]],
                   [0, 0, 1]])

alpha = np.deg2rad(22)
R = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])
R_ = np.array([[R[0, 0], R[0, 1], 0],
               [R[1, 0], R[1, 1], 0],
               [0, 0, 1]])

S_ =  np.array([[1.5, 0, 0],
               [0, 1.5, 0],
               [0, 0, 1]])

K_ =  np.array([[1, 0, 0],
               [0, 1, -1.5],
               [0, 0, 1]])



q_ = K_ @ T_ @ R_ @ S_ @ T_inv_ @ p_.T
q_ = q_.T

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q_[idx, 0], q[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

A fenti transzformációs mátrixok komponálása kompaktabb módon is elvégezhető:

p = np.array([[1, 1, 1], [2, 1, 1], [2, 2, 1], [1, 2, 1]])
idx = [0, 1, 2, 3, 0]

T_ = np.eye(3)
T_[:2, 2] = np.mean(p[:, :2], axis=0)

alpha = np.deg2rad(22)
R_ = np.eye(3)
R_[:2, :2] = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])

S =  np.eye(3) * 1.5
S[2,2] = 1

K = np.eye(3)
K[1, 2] = -1.5

q_ = K @ T_ @ R_ @ S @ np.linalg.inv(T_) @ p.T
q_ = q_.T

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q_[idx, 0], q_[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

Helmert transzformáció

A geodéziában gyakran előforduló egy ún. hétparaméteres vagy Helmert transzformáció mely megadható az alábbi alakban:

\( q = sRp + t \)

p = np.array([[1, 1, 1], [2, 1, 1], [2, 2, 1], [1, 2, 1]])
idx = [0, 1, 2, 3, 0]

alpha = np.deg2rad(22)
R_ = np.eye(3)
R_[:2, :2] = np.array([[cos(alpha), -sin(alpha)], [sin(alpha), cos(alpha)]])

S_ =  np.eye(3) * 1.5
S_[2,2] = 1

K_ = np.eye(3)
K_[1, 2] = -1.5

q_ = K_ @ R_ @ S_ @ p.T
q_ = q_.T

plt.figure(figsize=(3, 3))
plt.plot(p[idx, 0], p[idx, 1], 'r.-')
plt.plot(q_[idx, 0], q_[idx, 1], 'b.-')
plt.grid()
plt.gca().set_aspect('equal')

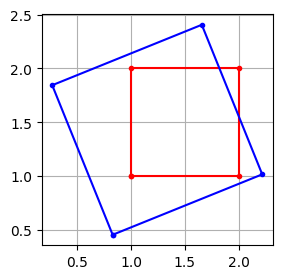
Vegyük észre, hogy a forgatás és skálázás referencia pontja a koordinátarendszer origója. A Helmert transzformációt leíró homogén transzformációs mátrix:

H_ = K_ @ R_ @ S_
print(H_)

[[ 1.39077578 -0.56190989  0.        ]
 [ 0.56190989  1.39077578 -1.5       ]
 [ 0.          0.          1.        ]]

Transzformációk térben

p = np.array([[0, 0, 0], [0, 0, 10], [0, 10, 10], [0, 10, 0], [0, 0, 0]])

ax = plt.figure().add_subplot(projection='3d')
ax.plot(p[:, 0], p[:, 1], p[:, 2], 'r.-')

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fb39132c310>]

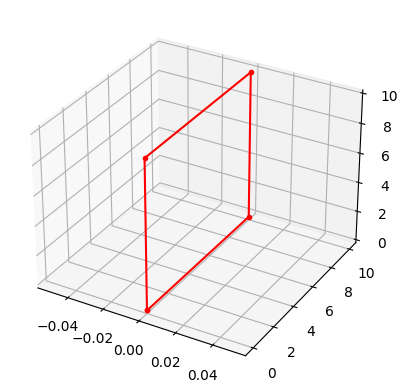
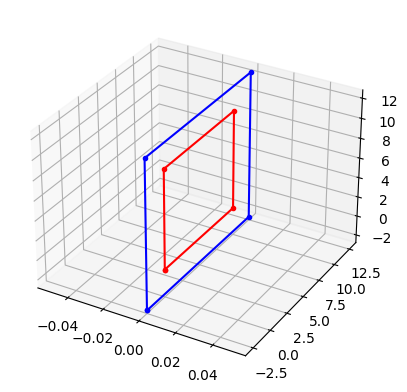
Eltolás és skálázás térben

Az eltolást és skálázást ugyanolyan módon tudjuk elvégezni mint síkon, az egyetlen különbség, hogy 3D koordinátákkal dolgozunk. Nézzünk egy példát, hogyan tudjuk a 3D négyszöget másfelészeresére nagyítani saját súlypontjából nézve:

p = np.array([[0, 0, 0], [0, 0, 10], [0, 10, 10], [0, 10, 0]])
idx = [0, 1, 2, 3, 0]

t = np.mean(p, axis=0)
q = 1.5*(p - t) + t

ax = plt.figure().add_subplot(projection='3d')
ax.plot(p[idx, 0], p[idx, 1], p[idx, 2], 'r.-')
ax.plot(q[idx, 0], q[idx, 1], q[idx, 2], 'b.-')

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fb3912469a0>]

Ezen transzformációk homogén koordinátákkal is leírhatóak a síkban bemutatott módon, a különbség, hogy a térbeli esetben a transzformációs mátrix \(4\times4\)-esek.

p = np.array([[0, 0, 0], [0, 0, 10], [0, 10, 10], [0, 10, 0]])
p_ = np.hstack((p, np.ones((p.shape[0], 1))))
idx = [0, 1, 2, 3, 0]

T_ = np.eye(4)
T_[:3, 3] = np.mean(p, axis=0)

S_ = np.eye(4)
S_[0, 0] = 1.5
S_[1, 1] = 1.5
S_[2, 2] = 1.5

q_ = T_ @ S_ @ np.linalg.inv(T_) @ p_.T
q_ = q_.T

ax = plt.figure().add_subplot(projection='3d')
ax.plot(p_[idx, 0], p_[idx, 1], p_[idx, 2], 'r.-')
ax.plot(q_[idx, 0], q_[idx, 1], q_[idx, 2], 'b.-')

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fb39132ed90>]

Forgatások

Kísérleti szögek teszteléshez:

euler_deg = [45, 15, -25]

yaw = euler_deg[0] / 180.0 * np.pi
pitch = euler_deg[1] / 180.0 * np.pi
roll = euler_deg[2] / 180.0 * np.pi

R_x = np.array([[1, 0, 0], [0, np.cos(yaw), -np.sin(yaw)], [0, np.sin(yaw), np.cos(yaw)]])
R_y = np.array([[np.cos(pitch), 0, np.sin(pitch)], [0, 1, 0], [-np.sin(pitch), 0, np.cos(pitch)]])
R_z = np.array([[np.cos(roll), -np.sin(roll), 0], [np.sin(roll), np.cos(roll), 0], [0, 0, 1]])

R = R_z @ R_y @ R_x
print(R)

[[ 0.8754261   0.46470208 -0.1329704 ]
 [-0.40821789  0.56351187 -0.71820089]
 [-0.25881905  0.6830127   0.6830127 ]]

A fenti forgatás megadható a scipy könyvtár Rotation osztályának segítségével:

from scipy.spatial.transform import Rotation
R = Rotation.from_euler('xyz', euler_deg, degrees=True)
print(R.as_matrix())

[[ 0.8754261   0.46470208 -0.1329704 ]
 [-0.40821789  0.56351187 -0.71820089]
 [-0.25881905  0.6830127   0.6830127 ]]

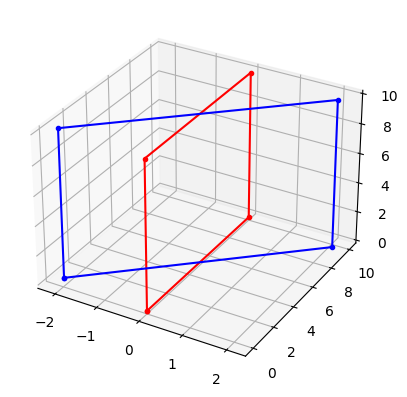
Forgassuk el a korábbi négyszöget 25 fokkal az órajárással megegyező irányban a Z tengely körül az alakzat súlypontja körül:

p = np.array([[0, 0, 0], [0, 0, 10], [0, 10, 10], [0, 10, 0]])
p_ = np.hstack((p, np.ones((p.shape[0], 1))))
idx = [0, 1, 2, 3, 0]

T_ = np.eye(4)
T_[:3, 3] = np.mean(p, axis=0)

euler_deg = [0, 0, -25]
R_ = np.eye(4)
R_[:3, :3] = Rotation.from_euler('xyz', euler_deg, degrees=True).as_matrix()

q_ = T_ @ R_ @ np.linalg.inv(T_) @ p_.T
q_ = q_.T

ax = plt.figure().add_subplot(projection='3d')
ax.plot(p_[idx, 0], p_[idx, 1], p_[idx, 2], 'r.-')
ax.plot(q_[idx, 0], q_[idx, 1], q_[idx, 2], 'b.-')

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7fb376c47c10>]

Belső és külső forgatások

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.transform import Rotation

# External imports
url = f"https://raw.githubusercontent.com/zkoppanyi/uni/main/utils/viz/viz.py"
!wget --no-cache --backups=1 {url}
from viz import plot_fustrum, plot_crs, set_3d_axes_equal

--2024-05-02 09:51:30--  https://raw.githubusercontent.com/zkoppanyi/uni/main/utils/viz/viz.py
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.109.133, 185.199.110.133, 185.199.111.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.109.133|:443... connected.
HTTP request sent, awaiting response... 

200 OK
Length: 2234 (2,2K) [text/plain]
Saving to: ‘viz.py’


viz.py                0%[                    ]       0  --.-KB/s               
viz.py              100%[===================>]   2,18K  --.-KB/s    in 0s      

2024-05-02 09:51:30 (33,4 MB/s) - ‘viz.py’ saved [2234/2234]

A következő függvény csinál nekünk grafikát, amiről értelmezni fogjuk a forgatásokat:

def plot_rotation(x, y, z, intrinsic=True):
    plt.figure(figsize=(9,7))
    ax = plt.axes(projection='3d')
    if intrinsic:
        R = Rotation.from_euler('XYZ', [x, y, z], degrees=True)
    else:
        R = Rotation.from_euler('xyz', [x, y, z], degrees=True)
    plot_fustrum(ax, [0, 0, 0], R.as_matrix(), img_limits=[1, 0.75], f=2.0, scale=1.0, c='k')
    plot_crs(ax, np.eye(3), X=[-2, -2, 0])
    crs = R.as_matrix().T
    plot_crs(ax, crs)
    set_3d_axes_equal(ax)

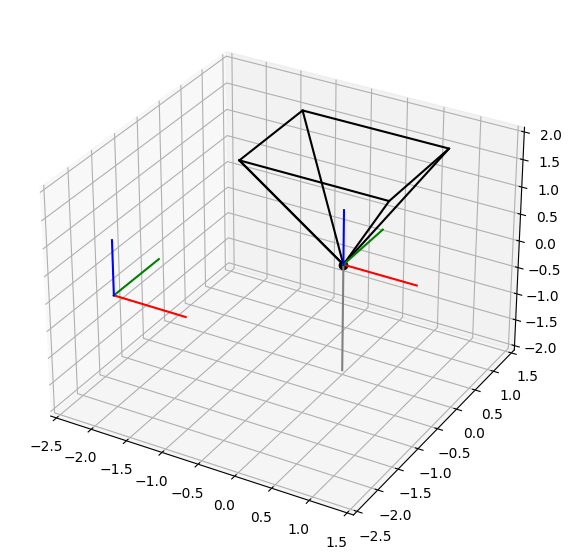
A grafika így nézz ki:

• pirossal az X tengelyt,

• zölddel az Y tengelyt, és

• kékkel a Z tengelyt láthatjuk.

plot_rotation(0, 0, 0)

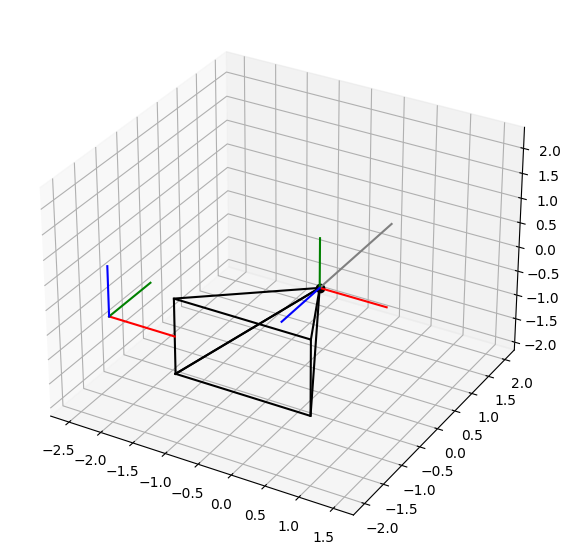
Forgatás az X tengely körül (piros tengely):

plot_rotation(90, 0, 0)

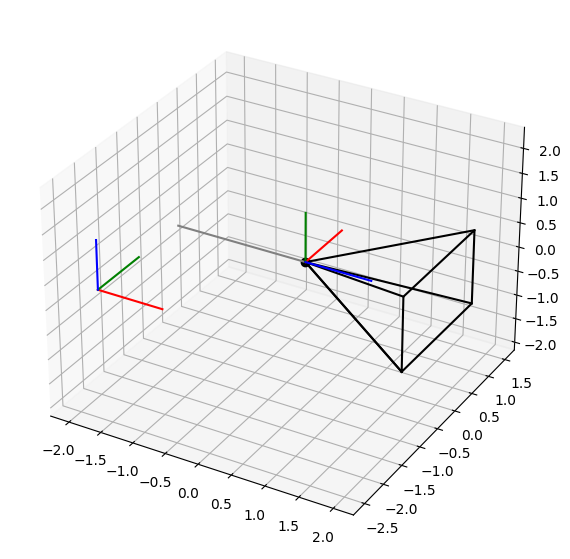
Forgatás az Y tengely körül az elforgatott koordináta rendszerben. Vegyük észre ez egy forgatás az X világbeli koordinátarendszerben.

plot_rotation(90, 90, 0)

Forgatás az Z tengely körül az elforgatott koordináta rendszerben. Ez egy forgatás az X világbeli koordinátarendszerben.

plot_rotation(90, 90, 90)

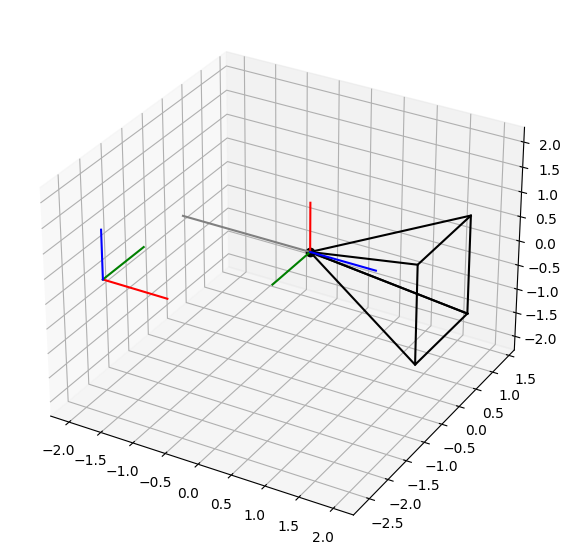
Magyarázat:

12 kombinációja van x, y, z tengelyek körüli forgatásnak:

• Mechatronikában használatos: z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y

• Navgiációban, fotogrammetriában használatos: x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z

További információ: https://en.wikipedia.org/wiki/Euler_angles#Definition_by_intrinsic_rotations

Oké, most nézzük meg ugyanezeket a forgatások külső forgatásoként.

Első forgatás az X tengely körül ugyanúgy nézz ki.

plot_rotation(90, 0, 0, intrinsic=False)

Vegyük észre, hogy a második forgatás viszont a világbeli Y tengely körül történik most.

plot_rotation(90, 90, 0, intrinsic=False)

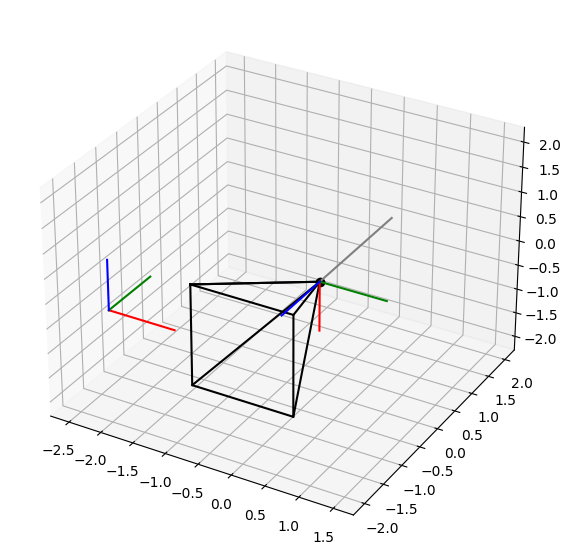
Ugyanígy a harmadik is.

plot_rotation(90, 90, 90, intrinsic=False)

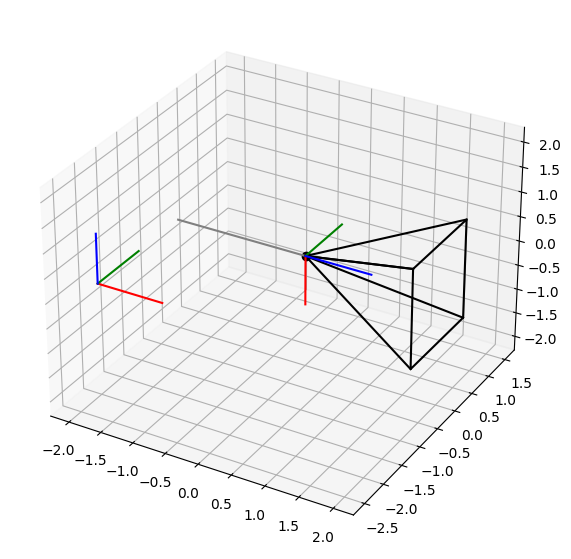
Tehát van 12 forgatás kombinációnk belső, illetve 12 forgatási kombinációnk külső forgatásokra. Ez összesen 24 különböző módja a forgatások definiálásának. Azonban ezek a forgatások nyilvánvalóan átfednek. Ennek módját a következő lemma adja meg.

Lemma: Egy Euler szögekkel adott belső forgatások ugyanazt a forgatást írják le, mint az ugyanazokkal a szögekkel megadott külső forgatások fordított sorrendje.

Ezt az ekvivalenciát deomnstrálja a következő kód.

# Test angle
rpy = euler_deg

# Rotation matrix from extrinsic rotations 
R_int = Rotation.from_euler('xyz', rpy, degrees=True) # extrinsic

# Reverse the order of the input Euler angles
ypr = [euler_deg[2], euler_deg[1], euler_deg[0]]

# Rotation matrix from intrinsic rotations of the reversed angle
R_ext = Rotation.from_euler('ZYX', ypr, degrees=True) # intrinsic

# Check whether the two are the same. 
chk = np.linalg.norm(R_int.as_matrix() - R_ext.as_matrix())
print(f"Difference of the two matrices: {chk}") # has to be small...

Difference of the two matrices: 0.0