Bevezetés a matplotlib könyvtárba

A matplotlib egy 2D és 3D függvények megjelenítéséhez, vizualizációjához használható könyvtár. Nevét onnan kapta, hogy a függvényeinek interfészei a matlabhoz hasonlóak.

A könyvtár együttműködik numpyval. A továbbiakban a plt aliasszal fogunk rá hivatkozni a kódokban:

import numpy as np
from matplotlib import pyplot as plt

Adatpontok megjelenítése

Olvassuk be a minta adata fájlt:

data = np.loadtxt('./data/path.txt')

Figyelem

Az adat fájlok elérhetőek a tantárgy honlapján!

Tekintsük meg a fájl első 5 sorát:

print(data[:5])

[[645779.76 272117.78]
 [645864.1  272075.3 ]
 [645910.56 272052.37]
 [645942.09 272030.22]
 [645982.8  271968.36]]

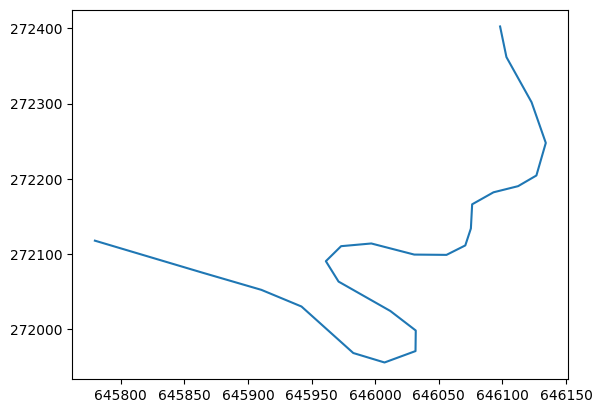
A fájl két oszlopból áll, melyek 2D pontok koordinátái. Ezek egy jármű útvonalának UTM koordinátái. Rajzoljuk ki az adatpontokat. Ehhez a Matlabhoz hasonlóan a plot függvényt használhatjuk, melynek a két bemeneti paramétere a koordináták. Ezután megjelenek az ábra.

from matplotlib import pyplot as plt
x = data[:, 0]
y = data[:, 1]

plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x7f8e37aa4c40>]

Tipp

Vegyük észre, hogy a matplotlib hasonló függvény paraméterekkel működik mint a Matlab, illetve hasonló logikán alapul maga a könyvtár is; innen a neve is. Így a Matlabban tanultakat használhatjuk itt is.

Vegyük észre, hogy az X és Y tengely arányai nem azonosak. Ezt a következő módon tudjuk javítani:

x = data[:, 0]
y = data[:, 1]
plt.plot(x, y)
plt.gca().set_aspect('equal')

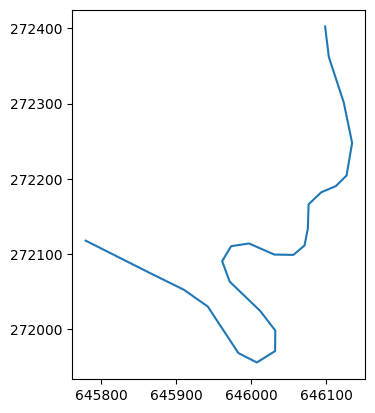
A fenti kód utolsó sora állítja be a helyes tengely arányokat (aspect ratio). A sor két függvényhívásból áll:

1. először lekérjük a tengelyekhez tartozó grafikus objektumot a gca() függvénnyel

2. ezután a set_aspect segítségével beállítható a tengelyek aránya. A set_aspect függvénynek további beállításai lehetnek

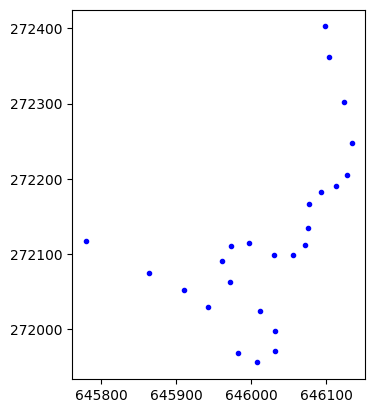
Alapértelmezetten a könyvtár összeköti az egyes adatpontokat. Amennyiben a pontokat mint pontok szeretnék a grafikán ábrázolni, formázzuk a grafikont a plot függvény harmadik paramétere segítségével:

from matplotlib import pyplot as plt
plt.plot(x, y, 'b.')
plt.gca().set_aspect('equal', 'box')

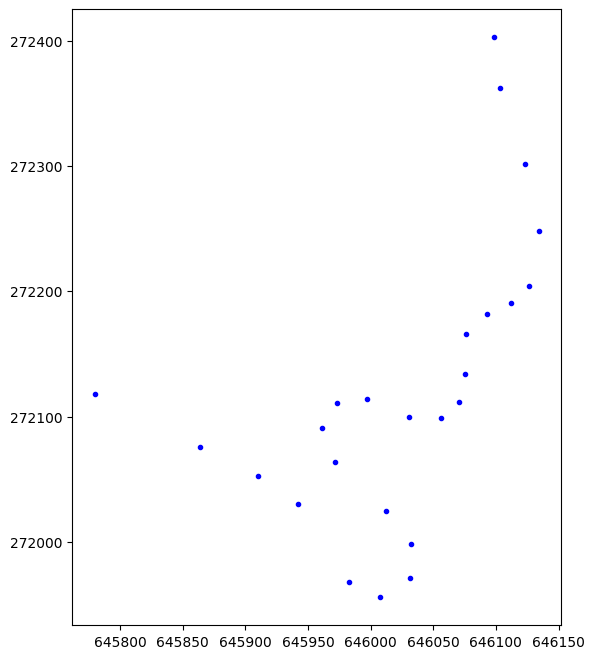
Az ábra méretét is megváltoztathatjuk a figure figsize paraméterének beállításával:

plt.figure(figsize=(10, 8))
plt.plot(x, y, 'b.')
plt.gca().set_aspect('equal', 'box')

További formázási lehetőség a pontokat összekötni:

from matplotlib import pyplot as plt
plt.figure(figsize=(10, 8))
plt.plot(x, y, 'b.-')
plt.gca().set_aspect('equal', 'box')

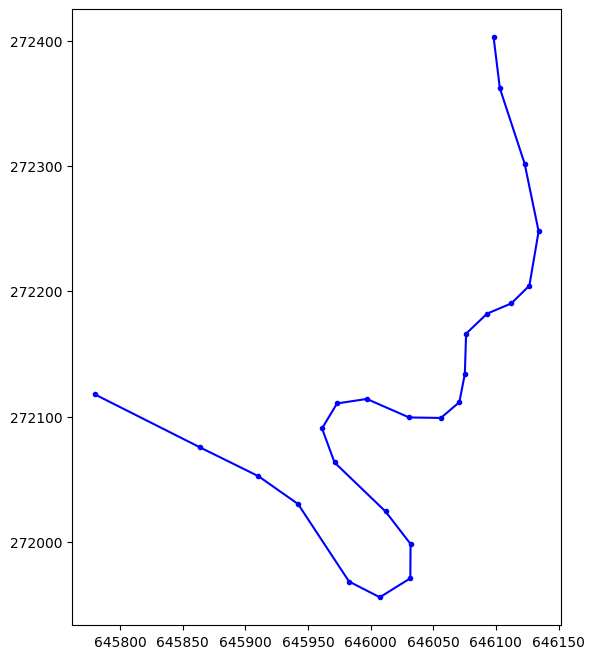
A formázás b.- három részből áll:

• b a színt jelöli,

• . a pont stílusát jelöli, amit markernek hívunk, és a

• - a vonal típusát jelöli.

További formázási lehetőségeket a help(plt.plot) parancs segítségével vagy a matplotlib honlapján találhatunk.

Feladat

A fenti ábrát jelenítsük meg szagatott vonallal és piros színnel. A pontokon jelenítsünk meg háromszöget.

Lehetőségünk van címet adni az ábrának a title függvény segtségével, mely az ábra fölé kerül alapértelmezésben. Ezen kívűl adhatunk jelmagyaráztatot is az ábrához. Ehhez adjuk meg label opcionális parametért a plot függvényhez, és hívjuk meg a legend függvényt az ábra kódja után.

from matplotlib import pyplot as plt
plt.figure(figsize=(8, 10))
plt.plot(x, y, 'r.--', label="Trajektória")
plt.gca().set_aspect('equal', 'box')
plt.xlabel('X [m]')
plt.ylabel('Y [m]')
plt.title('Adatpontok')
plt.legend()

<matplotlib.legend.Legend at 0x7f8e355afee0>

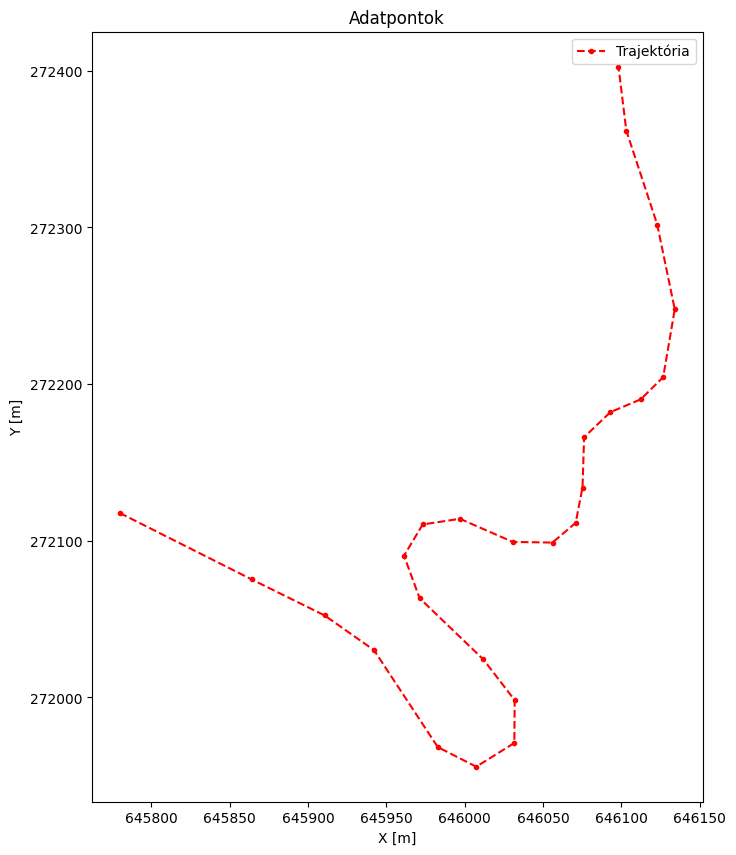
Függvények ábrázolása

Egy az analízis tárgyban tanult és hasznos csoportosítása a függvényeknek:

• Skalár-skalár függvények vagy egyváltozós valós függvények: Ezek a függvények az általonos iskolában tanult függvények, melyeknek bemenete egy szám, kimenete egy szám, vagy precízen fogalmazva a függvény értelmezési tartománya a valós számtest, és érték készlete is a valós számtest. A függvények definíció szerinti tulajdonsága, hogy egy bemeneti értékhez csak egy kimeneti érték tartozhat, de egy kimeneti értékhez több bemeneti érték is, vagy precízen, egy értelmezési tartománybeli elemet a függvény pontosan egy darab értékészlet beli elemre képez le. Ezt a matematikábn szürjektív leképezének hívják. Így például a kör nem adható meg skalár-skalár függvény formában, hiszen, például az origó középpoontú egység sugarú kör az X=0 pontban az Y=1 és Y=-1 pontokat venné fel, mely sérti a szürjektivítást.

• Skalár-vektor függvények vagy görbék: Ezek a függvények adnak meg tetszőleges görbét a síkon, vagy magasabb dimenziós térben. Bemenete egy szám, kimenete egy adott dimenziós vektor, vagy precízen fogalmazva a függvény értelmezési tartománya a valós számtest, és érték készlete a adott dimenziójú valós vektor tér. A bemeneti változót hívjuk a görbe paraméterének. Példaként említhetjük a kört, spirált, vagy akár az egyenes is megadható ebben a formában.

• Vector-skalár függvények vagy felületek: Ezek a függvényekkel adhatunk meg felületeket, például sík, ellipszoid, geoid, domborzat. A bemenete egy vektor a kimenete pedig egy szám, vagy precízen fogalmazva a függvény értelmezési tartománya egy adott dimenziójú valós vektor tér, és érték készlete a valós számtest.

• Vektor-vektor függvények vagy vektor mezők: Ezen függvények bemenete egy adott dimenziójú vektor, és kimenete ugyancsak egy vektor, melynek dimenziója eltérhet a bemeneti vektor dimenziójától. Precízen fogalmazva a függvény értelmezési tartománya és érték készlete a valós vektor téren van definiálva. A bemeneti változót hívjuk a görbe paraméterének. Vektormezőre példa a gravitációs erőtér, mely megadja a Föld egy adott pontján (bemeneti vektor) a gravitáció irányát és nagyságát (kimeneti vektor).

A függvények másik osztályozása a következő mely mérnöki gyakorlatban, vagy számítógépes gyakorlatban hasznos:

• explicit függvény,

• implicit függvény,

• parametrikus függvény.

Egy geometriai alakzat általában több különböző egyenlettel is megadható, melyek különböző függvény csoportokhoz tartozhatnak. Így például, a gömb egyenlete megadható implicit formában, ekkor ez az egyenlet skalár-vektor függvény, vagy megadható parametrikus formában, mely függvény vektor-vektor függvény csoportba tartozik.

Skalár-skalár vagy egyváltozós függvények ábrázolása

Ábrázoljunk egy másodfokú görbét (\(x^2\)) grafikonon. A függvény ábrázolásához generálnunk kell \((x, y)\) koordináta párokat. Ehhez szükségünk van a független változó egy sorára. A numpy könyvtár linspace függvényét használjuk:

x = np.linspace(-10, 10, 100)
y = x**2

print(x[:10])
print(y[:10])

[-10.          -9.7979798   -9.5959596   -9.39393939  -9.19191919
  -8.98989899  -8.78787879  -8.58585859  -8.38383838  -8.18181818]
[100.          96.00040812  92.08244057  88.24609734  84.49137843
  80.81828385  77.22681359  73.71696766  70.28874605  66.94214876]

Ezután jelenítsük meg a generált pontpárokat:

plt.plot(x, y, 'r-')

[<matplotlib.lines.Line2D at 0x7f8e35981490>]

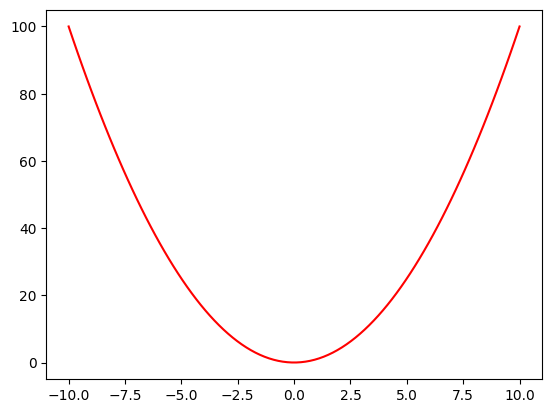
A függvényt definálhatjuk lambda segítségével is:

f = lambda x: pow(x, 2)
x = np.linspace(-10, 10, 100)
plt.plot(x, f(x), 'r-')

[<matplotlib.lines.Line2D at 0x7f8e357d3dc0>]

A linspaceben használt felosztás befolyásolja a függvény vizualizációjának a “felbontását”. Nézzük meg a következő példát, ahol 20, 10, 7 és 5 felosztás mellett jelenítjük meg a másodfokú görébt különböző. A különböző felosztások különböző színnel kerülnek megjelenítésre.

x = np.linspace(-10, 10, 20)
ax = plt.plot(x, f(x), 'k-')
x = np.linspace(-10, 10, 10)
ax = plt.plot(x, f(x), 'b-')
x = np.linspace(-10, 10, 7)
ax = plt.plot(x, f(x), 'g-')
x = np.linspace(-10, 10, 5)
ax = plt.plot(x, f(x), 'r-')

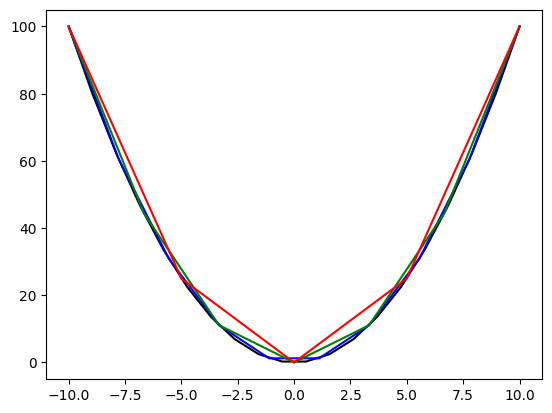
Látható a különbség a függvénye alakjában különböző felbontások mellett.

Hogy mennyire fontos a megfelelő felosztás megválasztása, azt az alábbi példa szemlélteti. Itt először a \(sin(10x)\) görbét rajzoljuk ki 10-es felosztással a \([-\pi, \pi]\) intervallumon.

f = lambda x: np.sin(10*x)
x = np.linspace(-np.pi, np.pi, 10)

plt.figure(figsize=(14,5))
ax = plt.plot(x, f(x), 'r-')

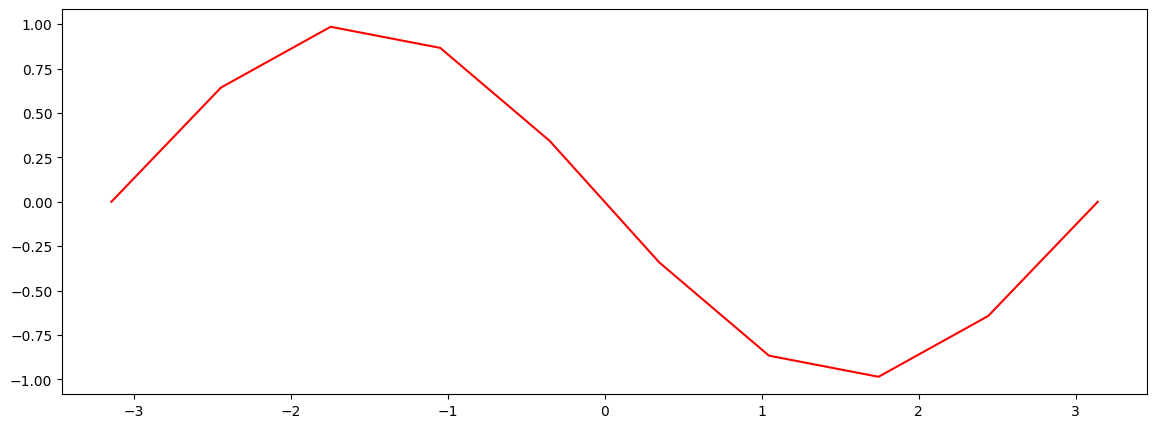
Ez alapján, azt gondolhatjuk, hogy a függvény alakja egy egyszerű szinus függvény. Most nézzük meg, mit kapunk 20 és 1000-es felbontás mellett

f = lambda x: np.sin(10*x)

plt.figure(figsize=(14,5))

x = np.linspace(-np.pi, np.pi, 1000)
ax = plt.plot(x, f(x), 'k-')
x = np.linspace(-np.pi, np.pi, 20)
ax = plt.plot(x, f(x), 'g-')

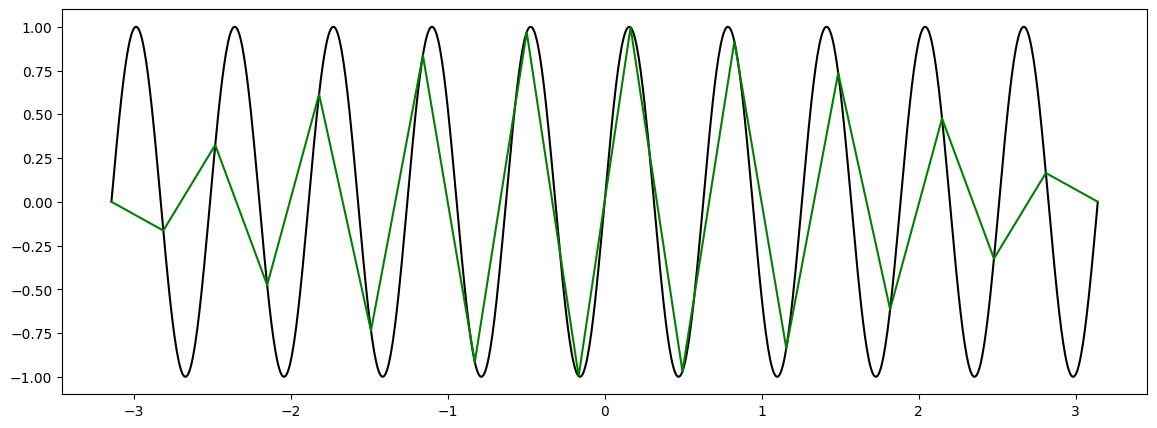
20-as felbontás esetén már láthatóak a csucsok, azonban a grafikon végein “lecsengés” látszik ami nem igaz. 1000-es felbontás mellett kapjuk meg a függvény igazi alakját. Emiatt legtöbb esetben célszerű nem felosztást, hanem lépésközt megadni, amihez az arange függvényt használhatjuk. Ebben az esetben is azonban óvatosnak kell lennünk bonyolultabb függvények esetén. Az alábbi példában 0.01-t használjuk lépésköznek:

x = np.arange(-np.pi, np.pi, 0.01)

plt.figure(figsize=(14,5))
ax = plt.plot(x, f(x), 'k-')

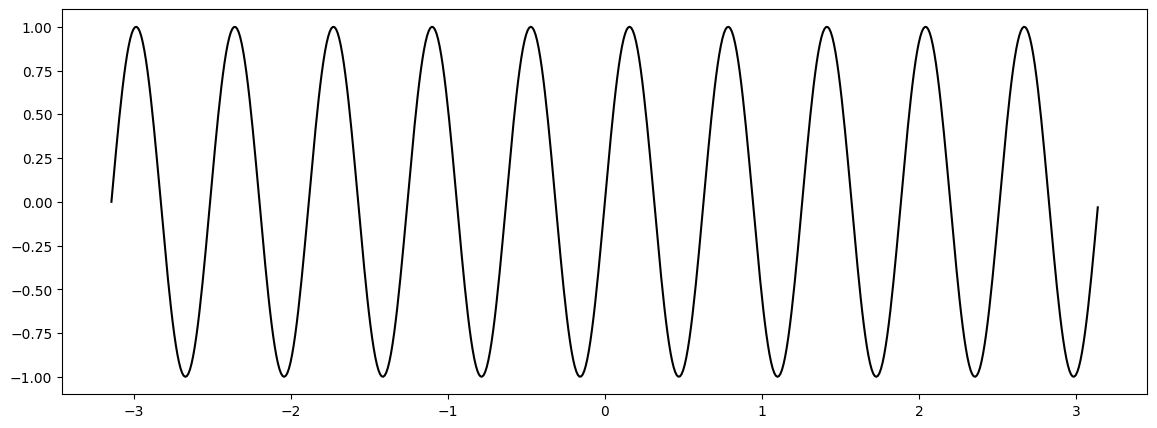
Vektor-skalár függvények a síkon

Ábrázoljuk a következő parametrikus (vektor-skalár) függvényt:

\(x = 2cos(t)\)

\(y = 2sin(t)\)

Ehhez a két koordináta függvényt definiáljuk, mint skalár-skalár függvényt:

t = np.arange(0, 2*np.pi, 0.01)
x = 2*np.cos(t)
y = 2*np.sin(t)

plt.plot(x, y, 'r-')
plt.gca().set_aspect('equal', 'box')

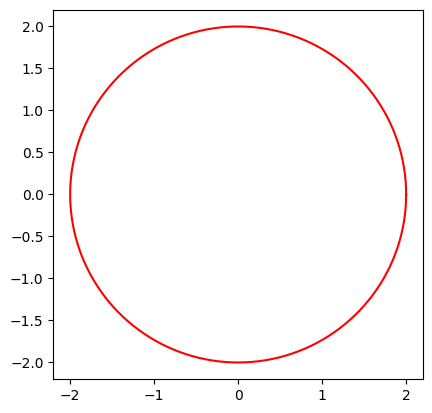
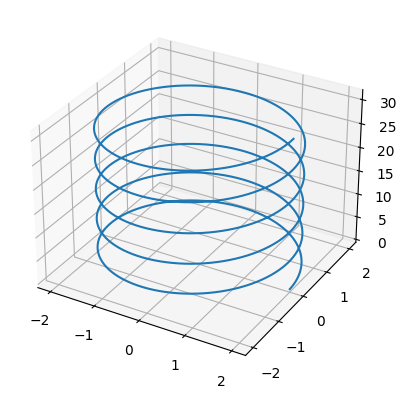
Parametrikus görbe a térben

ax = plt.figure().add_subplot(projection='3d')

t = np.arange(0, 10*np.pi, 0.01)
x = 2*np.cos(t)
y = 2*np.sin(t)
z = t

ax = plt.figure().add_subplot(projection='3d')
ax.plot(x, y, z)

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7f8e344d1c10>]

Kiegészítő anyag

Python vizualizációhoz további hasznos linkek:

• Matplotlib példák

• Szép 2D grafikák készítéséhez példák kóddal

• Seaborn könyvtár még szebb ábrákhoz és adat vizualizációhoz